Eléments d'épidémiologie médicale

L'épidémiologie clinique est la science de la prise de décision optimale en médecine clinique en fonction des caractéristiques épidémiologiques du malade, de son environnement et de sa pathologie.

L’approche "médecin-patient" est une relation unique pour laquelle on ne peut définir de "patient moyen" ni une démarche standard… De facto, on applique des traitements sur base de l'autorité (apprentissage, avis et textbooks), d'une rationalité evidence-based (guide-lines et revues evidence-based) et de nos croyances (expérience personnelle)… sans savoir si le patient y répondra.

L’approche de population (d’une ville, d’un hôpital,…) est une approche épidémiologique définissant des caractéristiques partagées par les patients d'un groupe donné.

La démarche de l’épidémiologie clinique consiste à partir d’un patient pour le resituer dans sa population d’origine (ayant des caractéristiques moyennes) afin de proposer des moyens diagnostiques et thérapeutiques ainsi qu'un pronostic adaptés à cette population fondés sur des probabilités. De façon plus simple, elle permet d'adapter rationnellement nos pratiques à chaque patient sur base des caractéristiques de la (des) population(s) dont il est issu.

La compréhension de cet article suppose la connaissance d'éléments de base de statistiques.

Définitions et fondamentaux

Probabilités, populations et échantillons

En médecine, la plupart des événements ou des mesures ne peuvent être déterminés avec certitude. L'incertitude n’est cependant pas synonyme d’absence de connaissance ou d’indétermination totale : on peut déterminer un range de valeurs au travers du concept de probabilité permettant de tirer des inférences statistiques. 

Méthodes d’échantillonnage

Sur des populations entières : les recensements (rares)

Par le biais de sondages : représenter la population et en inférer les résultats à la population. Ces représentations peuvent être des :

• Echantillons aléatoires
• Echantillons non aléatoires
  • Le sondage aléatoire simple = élémentaire
    • Chaque individu de la population a la même chance de se retrouver dans l’échantillon.
  • Le sondage aléatoire systématique
    • Ici on va construire l’échantillon avec un pas d’échantillonnage k = N/ n, et on prend dans l’échantillon [x, x+k, x+2k,…, x+(n-1)k]
  • Le sondage aléatoire en grappes
    • On subdivise la population en sous-groupes (grappes : un ménage, les occupants d’un immeuble, employés d’une entreprise…). On tire ensuite au sort quelques grappes pour constituer l’échantillon, soit en choisissant x grappes entières, soit en prenant de façon aléatoire simple y individus dans chaque grappe, soit…
    • On peut également utiliser des "facteurs de correction de  grappes" selon la taille des différents sous-groupes.
    • Ici la probabilité de chaque individu de se retrouver dans l’échantillon n’est pas la même.
  • Sondages stratifiés
    • La population normale est divisée en différentes strates selon différents critères. On tire ensuite au sort x individus dans chaque strate. Il existe 2 sous-types :
      • Stratifié proportionnel à la taille
      • Stratifié non proportionnel à la taille
    • Différence avec les grappes : ici toute la population N sert de base de référence.

Caractéristiques de l’échantillonnage

• Représentativité : peu dépendante de la taille de l’échantillon, très dépendante de la méthode d'échantillonage
• Précision : dépendante de la taille de l’échantillon
• Unité d’échantillonnage = élément de l’échantillon sur lequel porte la mesure et l’observation = unité permettant de construire un échantillon
• Echantillon = sous-ensemble de la population. Ses paramètres peuvent servir d’estimation à ceux de la population échantillonnée s’il répond aux critères de représentativité.

Notions d'association et de causalité

Table de contingence

	Malade	Non malade	Total
Exposés au facteur de risque	A	B	N1
Non exposés au facteur de risque	C	D	N0
Total	M1	M0	T

Mesure de l’association

Prenons pour exemple une enquête prospective visant à déterminer si l'âge maternel est un facteur de risque (FR) de la mortalité maternelle au Niger. Soit la table de contingence suivante :

	Décédées	Non décédées	Total
< 19 ans	700	13300	14000
>19 ans	800	45200	46000
Total	1500	58500	60000

On détermine une incidence de mortalité chez les mères de < 19 ans de 5% (700/14000) et de 1,7% chez  les > 19 ans. Comment peut-on les comparer ?

Le risque relatif RR

Le RR est défini comme le rapport entre le risque d’apparition de la maladie dans le groupe exposé au facteur de risque et le risque d’apparition de la maladie dans le groupe non exposé à ce facteur.

RR = incidence1/ incidence2 = (a/ N1) / (c/ N0)

Mesure de la force de l’association :

• Si RR = 1 : absence de relation
• La relation est d’autant plus forte que le RR est éloigné de 1
• Si le RR > 1 : facteur de risque
• Si RR < 1 : facteur protecteur

Dans l'exemple, le RR est de 2,94. Un âge maternel < 19 ans apparaît donc comme un facteur de risque de mortalité.

Le rapport de cotes : le odd ratio OR

Sa définition varie selon le type d'étude :

• Dans les études de cas-témoins, on définit une cote d’exposition comme le rapport des cotes d’exposition chez le malade et chez le non malade. Elle traduit le risque lorsque l’on est malade d’avoir été exposé par rapport aux non malades.
  • OR = (a/ c) / (b/ d)
  • Utilité rétrospective : il s’agit d'une mesure du risque d’avoir été exposé lorsque l’on est déjà malade
• Dans les études de cohortes, on définit une cote de maladie comme le rapport entre les cotes d’apparition de la maladie chez les exposés et de non malades chez les non exposés. Il s'agit alors d'une mesure du risque de devenir malade lorsqu'on est exposé.

Mesures ou évaluation d’impact : Risque Attribuable (RA) et Fraction Etiologique du Risque (FER)

Impact sur le groupe exposé 

Dans notre exemple, nous soustrayons à l’incidence de mortalité des < 19 ans celle des > 19 ans. Il reste alors la surmortalité liée au jeune âge = le Risque Attribuable au FR pour le groupe exposé = le nombre de cas attribuable au FR chez les personnes exposées atteintes = nombre de cas qui pourraient être évités en cas de disparition du FR = surmortalité = (A/N1) – (C/N0)

La Fraction Etiologique du Risque pour le groupe exposé : FER = Risque attribuable pour le groupe exposé / risque absolu pour le groupe exposé = [ (A/N1) – (C/N0) ] / (A/N1). Elle estime la proportion de cas imputables au FR chez les sujets exposés = pourcentage de cas qui pourraient être évités chez les personnes exposées en cas de suppression du FR.

Dans notre exemple : la FERexp = (700/14000 – 800/46000) / (700/14000) = (0,05-0,017) / 0,05 = 66%

66% de la mortalité des accouchements des femmes de moins de 19 ans pourrait donc être évités s’ils avaient lieu après 19 ans.

Impact sur la population

Le Risque Attribuable au FR pour la population est le nombre de cas que l’on peut attribuer au FR dans la population générale. RApop = M1/T – C/N0

La Fraction Etiologique du Risque pour la population générale estime la proportion de cas qui pourrait être évitée en cas de suppression du FR. FER = RApop / Risque absolu pop = [ (M1/T) – (C/N0)] / (M1/T)

Dans ce cas, le RApop = 1500/60000 – 800/ 46000 = 0,8%

Et la FERpop = 0, 8% / (1500/60000) = 32%

32% de la mortalité des femmes accouchant au Niger pourrait donc être évitée si les accouchements avaient tous lieu après 19 ans. 

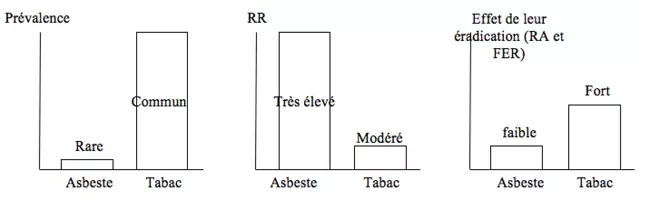
Exemple de relation entre RR, RA et FER d'un FR

Soit une étude sur la comparaison des effets de l’asbeste (amiante) et du tabac sur la mortalité… et sur les bénéfices de leur éradication. La détermination de ces paramètres démontre que l’effet positif à l’échelle de la population est plus important si l’on s’attaque à un FR de mortalité modéré mais fréquent (tabac) plutôt qu’à un FR de mortalité majeur (amiante) mais rare.

Interprétation des résultats d'une étude d'épidémiologie clinique

Quelles sont les questions à se poser face à une étude épidémiologique ?

• Y-a-t-il des erreurs (biais et précision) ?
• N’est-ce pas l’effet du hasard ?
• Les résultats ne sont-ils pas dus à autre chose (facteurs confondants) ?
• Existe-t-il une causalité dans l’association démontrée ?

Précision et validité (y-a-t-il des erreurs ?)

La validité est la capacité de l’étude à fournir une conclusion correcte (à traduire la réalité). Elle ne dépend pas de la taille de l’échantillon.

La précision se rapporte quant-à-elle à la fiabilité des mesures. Une étude peut être précise tout en étant biaisée : il faut s’assurer que les appareils et méthodes de mesures soient correctement réglés ou élaborées. La précision augmente avec la taille de l’échantillon.

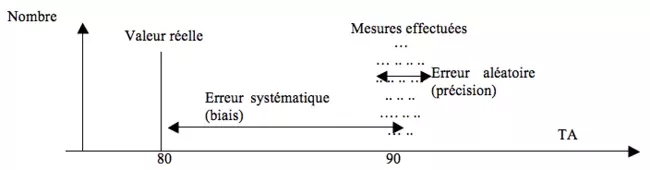
On peut ainsi distinguer deux types d’erreurs :

• Les erreurs aléatoires liées à la précision, que l’on peut minimiser en améliorant son matériel et ses méthodes et en augmentant la taille de l’échantillon.
• Les erreurs systématiques liées aux biais :
  • Biais de sélection (constitution de l’échantillon)
    • Minimisables par la standardisation du recrutement, la randomisation
  • Biais de mesure ou d’observation (récupération des données)
    • Minimisables par la pratique du double aveugle
  • (biais de confusion : cf facteurs confondants)

Précision et biais

Déterminer la part de hasard

Calcul d'un intervalle de confiance

On tire un échantillon (au hasard) et on en infère des résultats à la population… mais chaque échantillon donnera un résultat différent… comment peut-on être sûr de leur validité ? On construit un intervalle de confiance à 95% (risque d’erreur alpha = 5%) des échantillons… de manière à ce que l’intervalle contiennent la vraie moyenne de la population pour 95% des échantillons. 

Ex : une substance donnée soumet à un RR = 2 d’avoir un cancer du poumon… Cette différence est-elle réelle ou due à un hasard d’échantillonnage ? En construisant un intervalle à 95% : range de RR = 1,5 à 2,5 avec un risque de se tromper de 5%... tant que l’intervalle de RR ne contient pas 1 (le neutre pour un RR), on considère que l’association n’est pas due au hasard… s’il avait contenu 1 on aurait dû considérer qu’on aurait pu tomber sur un échantillon avec un RR = 1…

La fluctuation d’échantillonnage (longueur de l’intervalle de confiance) dépend inversement de la taille de l’échantillon, inversement de l’importance de l’erreur alpha et directement de la variabilité des observations (écart-type)

Test Ho

Cf l'article statistiques médicales.

Les facteurs confondants

Variables confondantes

On peut tenter d’exclure les variables confondantes potentielles par la randomisation.

Ex : étude voulant mettre en rapport l’incidence de la trisomie 21 avec la parité (nombre de grossesses antérieures). Une variable confondante certaine (déjà démontrée au préalable) est l'âge de la mère… ce dernier influant non seulement directement sur l’incidence de la trisomie 21 mais étant en sus en relation avec la parité... Une solution : faire une stratification des mères par âge.

Techniques de limitation de la confusion

• Lors de la préparation de l’étude
  • Randomisation
    • possible seulement pour les études prospectives, scénario de choix, répartit aléatoirement les différences (et donc les variables confondantes), mais moins efficace en cas de n petit (à compléter par restriction, en tenir compte lors de l’analyse)
  • Restriction (mais peut réduire la validité d’inférence des résultats à la population et rend plus difficile la constitution d’un échantillon)
  • Appariement (études cas-témoins)
• Lors de l’étude
  • Analyse multi-variée
    • Envisageable uniquement si tous les IC à 95% excluent tous 1.
  • Analyse stratifiée
    • Contrôler la confusion en évaluant l’association dans les catégories ou classes de la variable potentiellement confondante… puis en pondérant ses mesures.

Exemple dans une étude cas-témoins : 

	Malades (présentant un infarctus)	Témoins (n’ayant pas présenté d’infarctus)	Total
Prise d'une contraception orale (COC)	39	24	63
Pas de COC	114	154	268
Total	153	178	331

OR (odd Ratio) = 39/24 / 114/154 = 2,2 avec un IC à 95% [1,2-4.0]. Donc 2,2 x plus de gens ont été exposés aux COC parmi les malades que parmi les témoins. L’IC ne comprenant pas 1, on peut raisonnablement exclure le rôle du hasard.

Mais y a-t-il des variables confondantes (associées à l’exposition aux COC et favorisant la maladie) ?

On peut présumer que l’âge en soit une et diviser l’échantillon en 2 sous-groupes : les moins et les plus de 40 ans :

	COC	Malade	Témoin	OR	IC à 95%
Moins de 40 ans	+	21	17	2,8	1,2-6,7
	-	26	59
Plus de 40 ans	+	18	7	2,8	1,0-7,7
	-	88	95
Total	+	39	24	2,2	1,2-4,0
	-	114	154

Pour les moins de 40 ans, l’association est forte et significative. Pour les plus de 40 ans, l’association est forte mais non significative (l'IC comprend 1)… ce qui suggère la nécessité d'une étude avec un échantillon avec un n plus important (réduction de l’intervalle de confiance).

La causalité

Etablir une association significative entre la survenue de deux événements ne suffit pas à établir un lien de causalité (exemple type : il existe une association significative entre les infections à HIV [vecteur du SIDA] et à tréponème pallidum [vecteur de la syphilis]... l'une ne causant cependant pas l'autre !). Actuellement, on exige la présence de 8 critères pour établir une causalité :

• Temporalité
  • = La cause précède l’effet
• Plausabilité
  • Vraisemblable physiopathologiquement ? Cohérent avec l’histoire naturelle de la maladie ?
• Consistance, cohérence et validité des recherches
  • Observations répétées d’une association dans différentes populations, circonstances, études (des méthodologies différentes peuvent expliquer une absence de consistance)
• Association forte (RR élevé, OR)
  • Plus le RR ou le OR est faible, plus il y a de risques que les résultats soient influencés par des variables confondantes, biais… mais cela n’exclut cependant pas une relation causale
• Relation dose-réponse
  • En cas de relation causale, une augmentation de dose et/ ou de temps d’exposition induit généralement une augmentation des effets (fréquence de la maladie,...)
  • Cet argument est très important
• Réversibilité
  • Une diminution de dose et/ ou de temps d’exposition induit une baisse de risque (ex : l'arrêt du tabagisme entraîne une diminution importante du risque de cancer du poumon)
• Spécificité
  • Moins il y a de FR impliqués, plus leur rôle causal est vraisemblable
  • N’est jamais totale : les maladies sont généralement multicausales et les FR ont généralement des effets multiples
  • Ex : 90% des cancers du poumon surviennent chez les tabagiques
• Plan d’étude de qualité maîtrisant les variables confondantes
  • Essais contrôlés randomisés : forte
  • Etudes de cohorte : modérée (observation, pas de randomisation)
  • Cas-témoins : modéré (pas de garantie par rapport à la temporalité)
  • Etudes transversales : faible
  • Etudes écologiques : faible

Une relation de causalité peut exister même si tous les critères ne sont pas remplis (ex : typiquement la réversibilité n'est fréquemment pas rencontrée)… et certains critères sont plus importants que d’autres (ex : temporalité, relation dose-réponse). Il n'y a pas de formule pour établir une causalité, seulement du bon sens et de la logique.

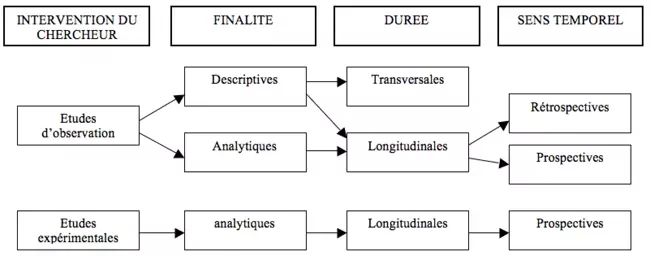
Types d'études épidémiologiques

Elles peuvent être classées selon : finalité, interventions du chercheur, calendrier (sens temporel), durée.

Types d'études épidémiologiques

Epidémiologie descriptive 

• Etudes d’observation – descriptive – transversale [= à un moment donné - sur un événement donné tel que l’embauche, l’entrée à l’école,…], longitudinale (rétrospective ou prospective) ou écologique
  • Une étude écologique consiste en une comparaison de groupes (pays de résidence, profession, statut socio-économique,…) plutôt que d’individus. Elle ne permet pas de lier un individu particulier à la conséquence (maladie, décès,…).
    • Ses avantages : calcul de coefficients de corrélation, données facilement disponibles, rapides, faible coût
    • Ses inconvénients : ne permettent pas d’émettre une hypothèse, ne permettent pas de contrôler les facteurs confondants, « ecologic fallacy » (la relation de groupe n’est pas forcément transposable à l’individu)
  • Les études transversales sont les plus nombreuses et permettent d’estimer la prévalence d’un problème.
• Résultats exploitables des études descriptives :
  • Calcul de proportions d’individus présentant ou ne présentant pas le problème, un comportement ou un facteur de risque
  • Formulation d’hypothèses sur base de calcul de mesures d’association (ex : OR entre consommation d’ecstasy et dépression), à confirmer via des études analytiques.

Epidémiologie analytique

Elles cherchent à établir une relation causale entre l’apparition d’une maladie et un facteur déterminé… 

• Etudes d’observations – analytiques – cohorte, cas-témoins, écologiques
• Etudes expérimentales (essais cliniques non randomisés, essais communautaires randomisés)

Etudes de cohorte

Etapes :

• Sélectionner un échantillon d’exposés et de non exposés
• Suivre les groupes sur une période
• Recueillir l’information concernant l’incidence du problème étudié

Analyse des résultats :

• Mesures d’association (RR, RA, FER, …)
• Eliminer le rôle du hasard (tests de signification statistique : comparaison de moyennes et de proportions, analyses de survie,…)

Avantages :

• Calcul de risque
• Informations sur l’incidence
• Pas d’ambiguité temporelle
• Expositions rares
• Survenue de plusieurs problèmes de santé (ex : alcool générant cirrhose, accidents, polyneuropathies,…)
• Etude de la relation dose-effet

Désavantages :

• Temps
• Coût
• Taille des échantillons
• Difficile pour les pathologies rares
• Possible perte de suivi
• Possibles changements d’exposition durant le suivi

Etudes cas-témoins

Etapes :

• Sélectionner un échantillon de cas parmi la population
• Sélectionner des « témoins » contrôles comparables
• Déterminer l’exposition dans les deux groupes de comparaison
• Recherche rétrospective de l’exposition

Ex : études sur l’aspirine comme FR pour le syndrome de Reye. On prend deux groupes : cas (ont eu Reye) et témoins (n’ont pas eu Reye) et on effectue une recherche rétrospective de la proportion des individus ayant été exposé à l’aspirine pour les cas et pour les témoins.

Avantages	Désavantages
Ok pour maladies rares Ok pour maladie avec longue latence Nécessite des échantillons moins grands Données d’accès facile Pas de problème éthique (déjà malades) Permet d’étudier plusieurs FR	On ne détermine pas le risque (incidence) Peu intéressant pour les expositions rares Biais de sélection ++ Biais de mesure de l’exposition (mémoire des patients) Limité à l’étude d’une seule maladie

Etudes expérimentales (interventionnelles)

Implique l'mposition de l’exposition dans

• Des conditions non contrôlées : pas de sélection des sujets (ex : vaccination à diminution de l’incidence de la maladie ?)
• Des conditions contrôlées : essais cliniques/ essais sur le terrain/ interventions communautaires
• Des conditions naturelles : « accidents » (ex : incident  nucléaire, guerre,…)

On distingue les :

• Etudes randomisées
  • Répartition aléatoire des participants dans les groupes, minimise les biais de confusion, nécessite au moins deux groupes (ex : sous médoc et sous placebo)
• Etudes non randomisées (= quasi-expérimentales)
  • Ex : essais communautaires (ex : fluorisation de l’eau) = mesurer l’impact d’une mesure sur la communauté sans essayer de faire un lien avec l’exposition individuelle

Ces études sont susceptibles de fournir d'excellents renseignements exploitables mais posent des problèmes éthiques +++

Epidémiologie clinique et démarche diagnostique

La pose d’un diagnostic peut se résumer à "est-on dans le normal ou l'anormal ?"

Approche de la normalité

Approche statistique de la population

Basée sur des courbes de Gauss… reflétant la distribution d’une variable dans la population. Dans cette optique la normalité est synonyme de norme. Ex : sur base d'une courbe de poids des adolesents des USA, on conclura qu’une surcharge pondérale correspond à la normalité.

Approche liée à la pathologie

On ne se base pas ici sur la majorité de la population mais sur un FR de pathologie. Ainsi, la majorité de la population présente des valeurs de cholestérol estimées bien trop élevées d’un point de vue physiopathologique (risque cardio-vasculaire majoré).

Courbe de Gauss cholestérol

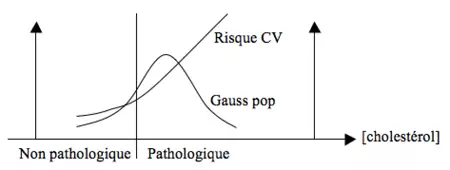
Dans certains cas il n’y a pas de recouvrement entre les valeurs pathologiques et non pathologiques. Le diagnostic est alors aisé. Ex : glutathion réductase (NADPH) :

Précision et biais

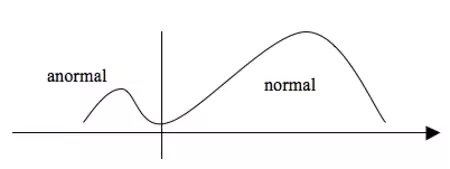
Cependant, dans la plupart des cas, on ne peut établir une telle limite : des valeurs très élevées d’enzymes cardiaques (semblant anormales) peuvent se rencontrer chez des sujets sains alors que des sujets présentant une réelle ischémie myocardique peuvent avoir des enzymes cardiaques basse = recouvrements.

La démarche diagnostique

Le clinicien se base sur les premiers signes et dires du patient pour élaborer un diagnostic différentiel "éclair" basé sur les probabilités. Au fil de l’anamnèse et de l’examen clinique, il exclura ou ajoutera l’une ou l’autre pathologie et augmentera ou diminuera les probabilités des différentes pathologies.

L’objectif est donc de passer d’un diagnostic basé sur des probabilités à priori à des probabilités à postériori.

La probabilité à priori dépend de :

• La prévalence des pathologies +++
• La spécificité des symptômes et signes

Les prévalences doivent ensuite être revues en fonction du contexte de vie du patient, de ses expositions aux FR, du contexte épidémiologique,… Il faudra ensuite estimer si l’incertitude qui persiste encore doit être levée par des tests et autres investigations. Le choix des différents examens devra donc être commandé en fonction de ce niveau d’incertitude. Problèmes : la liberté de choix diagnostique est de plus en plus mise à mal par les impératifs économiques… et la demande médicale croissante des populations dans les pays développés amènes de plus en plus de sujets "sains" à consulter.

Le crédit que le clinicien devra apporter aux différents résultats n’est pas aléatoire, il peut être quantifié à l’aide de différents paramètres liés au test, à la technique, à la mesure elle-même, au contexte… Le clinicien devra ensuite tenir compte de la variabilité inter-patient et de la variabilité des paramètres.

La plupart des tests offrent pour résultat des variables quantitatives continues, très variables et avec un recouvrement entre normalité et anormalité. Ces résultats sont par la suite transformés en variables dichotomiques (test positif ou négatif) selon des seuils fixés arbitrairement sur base de considérations sanitaires et économiques.

Situation de recherche (= Gold Standards)

Sensibilité et spécificité 

Tableau de contingence d'un test diagnostique :

	Malade	Non malade	Sous-total
Positif	a	b	a+b
Négatif	c	d	c+d
Sous-total	a+c	b+d	Total

On définit des mesures de performance du test (VP = "vrais positifs", VN = "vrais négatifs", FP = "faux positifs", FN = "faux négatifs") :

• Sensibilité (Se) = VP / (VP + FN) = a / (a+c)
• Spécificité (Sp) = VN / (VN + FP) = d / (b+d)

La sensibilité est la capacité à reconnaître comme malade celui qui est vraiment malade (= probabilité d’avoir un test postifi quand le patient est malade).

La spécificité est la capacité à reconnaître comme non malade celui qui n’est pas malade (= probabilité d’avoir un test négatif quand le patient n’est pas malade). 

Ces mesures, dépendant du seuil fixé de positivité, sont calculées en connaissant l’état des sujets (malades, non malades). Le rapport entre malades et non malades n’intervient pas (= la prévalence de la maladie n’est pas prise en compte).

Selon le but poursuivi, on peut modifier la sensibilité et la spécificité d’un test (changement de seuil). 

Sensibilité, Spécificité, seuil de positivité

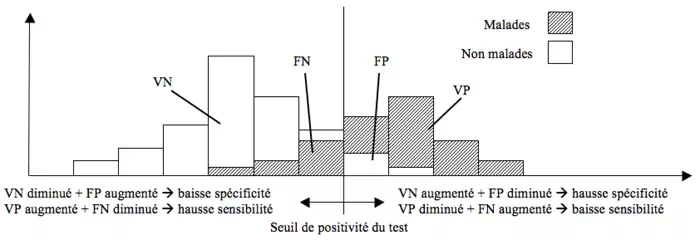
Augmenter la sensibilité d’un test revient donc à diminuer sa spécificité et inversement.

• Augmenter le seuil de positivité du test augmente la spécificité et diminue la sensibilité
• Baisser le seuil de positivité du test augmente la sensibilité et diminue la spécificité

Les courbes ROC et le choix d’un seuil

Une courbe ROC (Reveiver Operating Characteristic) est un graphique montrant le tracé des valeurs de la sensibilité en fonction de (1 -  la spécificité) pour chaque valeur seuil donnée.

Le « point le plus discriminant » correspond à celui qui présente la SSC (surface sous la courbe) la plus élevée. Le point idéal est le coin supérieur gauche (spécificité = sensibilité = 1). On choisira donc généralement le point de la courbe le plus proche du coin supérieur gauche. Cependant, ce point n'est pas toujours le plus apte à répondre à la question posée : il peut être important de privilégier la spécificité (traitement très toxique,…) ou la sensibilité (maladie à évolution fatale rapide,…).

Courbes ROC

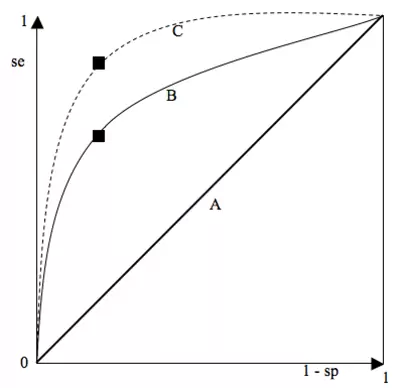
• Courbe A (diagonale d’égalité) : le meilleur point correspond à une sensibilité = spécificité = 0,5. Cette courbe correspond donc à un test totalement inefficace : il y a autant de gens sains déclarés malades que non malades et autant de gens malades déclarés sains que malades.
• Courbe B : correspond à la courbe de température comme test diagnostique pour la grippe. Le meilleur point correspond à une sensibilité = 0,65 et une spécificité = 0,75, valeurs déterminées pour un seuil de 39°C.
• Courbe C : correspond à un test presqu’idéal, permettant d’obtenir des valeurs très élevées de spécificité et de sensibilité. Ex : dosage des CK et infarctus myocardique.

La courbe ROC offre donc une estimation globale de la valeur d’un séparateur et peut comparer la valeur discriminante de deux tests.

Les rapports de vraisemblance : LR = Likelihood Ratio 

Autre moyen de résumer la sensibilité et la spécificité. Alternative à la courbe ROC

On définit :

• Le LR positif  = (sensibilité) / (1-  spécificité)
  • = proportion entre la probabilité d’avoir un test positif chez un malade et la probabilité d’avoir un test positif chez un non malade
• Le LR négatif = (1 – sensibilité) / (spécificité)
  • = proportion entre la probabilité d’avoir un test négatif chez un malade et la probabilité d’avoir un test négatif chez un non malade

Ces rapports de vraisemblances sont également indépendants de la prévalence et permettront de calculer les VPP (valeur prédictive positive) et VPN (valeur prédictive négative).

Ils offrent une aide précieuse à la décision diagnostique. Ex : un test avec un LR positif = 2,3 signifie que si le test est positif, il est 2,3 x plus probable que le patient soit malade plutôt qu’il ne le soit pas. Ex : un test avec un LR négatif = 0,2 à signifie que si le test est négatif, il est 0,2 x plus probable que le patient soit malade plutôt qu’il ne le soit pas (autrement dit : il est 5 x plus probable que le patient ne soit pas malade plutôt qu’il ne le soit).

La proportion de classification correcte = E = PCC

Peu utilisée. PCC = (VP + VN) / Total des patients. Elle varie de 0-1 (0,5 = hasard)

Indice de Jouden J

Peu utilisé. Compris entre -1 et 1. J = (sensibilité) + (1 – spécificité)

Situation de pratique clinique

En pratique, lorsque l’on reçoit le résultat d’un test, le statut malade/ non malade n’est pas connu : c’est ce que l’on cherche ! On doit intégrer la notion de prévalence (dépendante des FR et caractéristiques intrinsèques de la population). Ce qui intéresse le médecin peut s’exprimer ainsi : quelle est la probabilité de présence de la maladie chez ce patient, sachant que le test a donné un résultat positif ou négatif. Ces probabilités sont appelées valeurs prédictives.

Les valeurs prédictives

• La VPP = valeur prédictive positive = probabilité que le patient soit malade si le test est positif
  • VPP = VP / (VP + FP)
• La VPN = valeur prédictive négative = probabilité que le patient ne soit pas malade si le test est négatif
  • VPN = VN / (VN + FN)

Elles intègrent donc la notion de prévalence (dépend des proportions de malades et de non malades) et varient d'un centre à l’autre (prévalences des populations locales) et selon le temps. Les labos donnent donc les sensibilité et spécificité (car typiques de la maladie et du test, et non pas les valeurs prédictives). Les valeurs prédictives sont cependant très utiles pour l’usage au sein d’un centre (population) donné, particulièrement si cette population a une prévalence très particulière (ex : toxicomanes ayant une prévalence HIV +++). La VPP augmente (ou diminue) si la prévalence augmente (ou baisse), la VPN augmente (ou diminue) si la prévalence baisse (ou augmente).

Ex : test pour dépister les HIV + dont les sensibilité (97%) et spécificité (99,8%) sont fixes

Au sein d'une population non toxicomane donnée dont la prévalence d’HIV + = 0,3%, pour mille patients :

Sensibilité = a/ a+c → a = 97% x 3 = 3 (quasi)

Spécificité = d / b+d → d = 99,8% x 997 = 995

	HIV +	HIV -	Total
Test +	3	2	5
Test -	0	995	995
Total	3	997	1000

VPP = 3 / (3 + 2) = 60%

VPN = 995 / (995+0) = 100% (quasi)

Conclusions :

• Sur 100 patients ayant un test positif, 60 seront vraiment malades, mais 40 ne le seront pas !
• Sur 100 patients ayant un test négatif, (quasi) 100 seront vraiment sains !
• Pour une telle population, on peut sans crainte annoncer une séronégativité en cas de test négatif… par contre en cas de test positif, on ne peut rien annoncer… Que faire de ces patients ?

Une VPN forte est donc utile si l'on veut exclure une maladie

Chez une population toxicomane donnée dont la prévalence d’HIV + = 60%, pour mille patients :

Sensibilité → a =  97% x 600 = 582

Spécificité → d = 99,8% x 400 = 399

	HIV +	HIV -	Total
Test +	582	1	583
Test -	18	399	417
Total	600	400	1000

VPP = 582 / (582 + 1) = 99,8%

VPN = 399 / (399 + 18) = 95,7%

Conclusions :

• Sur 100 patients ayant un test positif, 99,8 seront vraiment malades
• Sur 100 patients ayant un test négatif, 95,7 seront vraiment sains
• En pratique, dans les deux cas on pourra annoncer les résultats du test (même si 3 % des HIV+ échapperont au dépistage…)

Une forte VPP est donc utile pour confirmer un diagnostic.

Un même test, signe ou mesure… peut donc avoir une valeur diagnostique toute différente selon le contexte épidémiologique (prévalence de la maladie) → nécessité d’une bonne anamnèse avec une bonne identification des facteurs de risque pour pouvoir identifier les population cibles d’un test diagnostique ou de dépistage !

Il est donc absurde de demander un test HIV pour un patient sans FR : que dira-t-on aux patients ayant un test positif, sachant qu’il y a 40% de chance qu’ils soient sains ! Il est tout aussi absurde de demander une VS "de routine" en l’absence de facteurs faisant suspecter une inflammation : une VS élevée chez un patient présentant des lésions cutanées associées à des arthralgies chroniques nous incitera à demander une recherche d’auto-anticorps pour exclure une vasculite… mais que faire d’une VS positive lors d'un "bilan de routine" ? Les chances que cette VS ne représente rien de pathologique sont tellement élevées que l’on ne fera rien du tout et ce test, onéreux, était totalement inutile, voir pire nous amènera à demander des examens complémentaires de seconde ligne, plus onéreux et plus invasifs, dont la signification sera tout aussi improbable !

Une autre application directe de ces considérations consiste en un recours différencié aux examens complémentaires par les généralistes et les spécialistes. En effet, les généralistes sont confrontés à des prévalences faibles des pathologies, les spécialistes (dont les patients sont normalement déjà passés par plusieurs filtres ou présentent des pathologies plus souvent chroniques) à des prévalences hautes. Les spécialistes tireront donc plus d’avantages des examens complémentaires que les généralistes. Cette réalité est malheureusement en train de se modifier dans les pays développés, les patients ayant de plus en plus recours aux spécialistes de leur propre initiative... fait, combiné aux habitudes bien ancrées des spécialistes, amenant à la croissance des examens revenant négatifs et des examens positifs difficiles à corréler à une significaiton clinique.

Calcul des valeurs prédictives

1° Au moyen du tableau de contingence (grâce aux sensibilité, spécificité et prévalence, cf les définitions et exemples du point précédent)

2° Au moyen du théorème de Bayes (théorème de l’inversion des probabilités conditionnelles)

Théorème de Bayes : si on connaît la probabilité que B soit vrai quand A est vrai, alors on peut connaître la probabilité que A soit vrai quand B est vrai. Soit :

(Proba A soit vrai si B est vrai) = [(Proba B soit vrai si A est vrai) x (Probabilité que A soit vrai)] / [[(Proba B soit vrai si A est vrai) x (Probabilité de A)] + [(Probabilité que B soit vrai quand A est faux) x (Probabilité que A soit faux)]]

→ Si on connaît la probabilité d’avoir un test positif (B) quand le patient est malade (A) (= sensibilité) alors on peut connaître la probabilité d’être malade quand le test est positif (= VPP).

VPP = (sensibilité x prévalence) / (sensibilité x prévalence +  [1-spécificité] x [1- prévalence])

Il faut donc préalablement connaitre les sensibilité, spécificité et prévalence.

3° Au moyen des LR

Démarche :

• On part de la prévalence
• On calcule la cote de pré-test (= prétest odds = cote de prévalence) = prévalence / (1- prévalence)
• On calcule la cote de post-test = cote de pré-test x LR positif
• On calcule la VPP = cote de post-test / (cote de post-test + 1)

En pratique on utilise des tables pré-établies donnant la VPP en fonction de la prévalence et du LR positif

Ex : anémie et consultation prénatale dépistée par tigette (sensibilité = 90%, spécificité = 85%)

• La prévalence de l’anémie chez les femmes enceintes est de 50%
• Cote de pré-test = 0,5/ 1-0,5 = 1
• LR positif = sensibilité / (1 – spécificité) = 0,9 / 0,15 = 6
• Cote de post-test = 1 x 6 = 6
• VPP = 6 / 7 = 86%

Cela signifie que l’on est passé d’une probabilité diagnostique à-priori de 50% (prévalence de l’anémie chez les femmes enceintes) à une probabilité diagnostique à-postériori (après le test) de 86% (VPP).

On recherche donc une succession de tests capables de faire monter la VPP (réduire l’incertitude). Un bon test diagnostic est donc d’un point de vue de santé publique celui qui offre la meilleure réduction d’incertitude au moindre coût.

Auteur(s)

Dr Shanan Khairi, MD